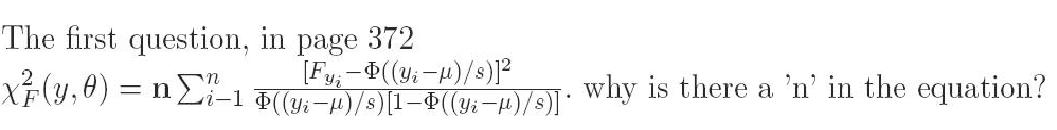
Reader's questions

    1. "n" in page 372

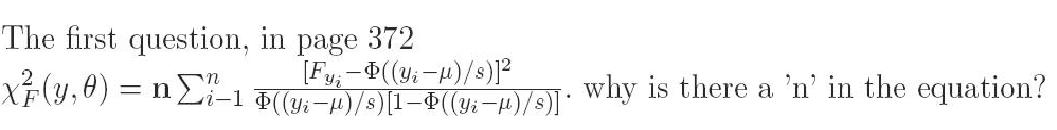
    REPLY: n comes from the variance of the sample binomial proportion which is var(p) = p(1-p)/n; where p here is substituted by F(y_i|θ)

    2. What is the association between y.rep and ordered.y.rep and their expected scale in terms of posterior means (in example 10-3).

    REPLY:

ordered.y.rep are y.rep but they are in ascending ordering order (within each iterations). So ordered.y.rep[1] is the smallest y.rep in each iteration, ordered.y.rep[2] is the 2nd smallest y.rep in each iteration  etc. The means of the first will centered to the sample mean (which is close to zero here) while the second to the corresponding i/n percentile of the distribution assumed by the model.

    3. What is the difference of IPPO and CPO?

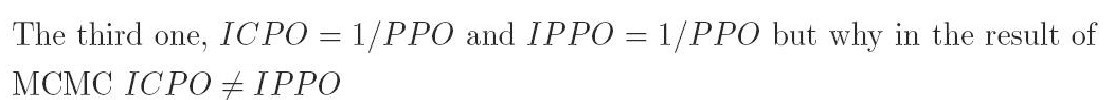
    REPLY:

cpo = [mean(1/ppo)]^{-1}

ippo = 1/mean(ppo)

[there is no clear explanation what ippo stands for in table 10.24]

 

    4.  NAs in zero-ones trick

I have a question about the use of the zero-one trick. I don't know how to use the zero-one trick to estimate values for the missing data. If you have time, please provide your comments, which I would really appreciate.

Just for an instance,  I generated 20 data from a normal distribution with mean = 10 and sd = 1, but one data was missing. The following program is simply not able to estimate values  for the missing data. Could you please help me out, showing me how to estimate values for this missing data?

    REPLY:

the zero-ones trick works only for known data. 

in order to make it work in your case you need to define that x[i] ~ uniform distribution in sufficiently large interval when x[i] is NA.

 

I think this will work. (if I remember correctly)

 

 

     5.  Covariance structure on dispersion parameters

Now I'm trying to fit negative binomial model but I see, when looking at the pearson's residual vs. fitted values, that the variance is clearly getting smaller as the fitted values increase. In order to deal with this I'm trying to add a structure to the dispersion parameter `r`. You have mentioned in your book that  this is possible but I'm looking for an example. Can I just add a linear structure to r? such as:

 

r[i]<-inprod(alpha.r[1:4],X[i, 1:4]) + inprod(beta.r[1:4], X[i,1:4]*lambda[i])

    REPLY:

If the dispersion parameter is positive then use log r otherwise you will have trap problems  since in some iterations the dispersion may take negative values with the above linear structure.

 

 You may possibly also have the problem that winbugs cannot select update method (especially if the likelihood is no longer log-concave).